선형 회귀(Linear Regression)
선형 회귀는 주어진 데이터로부터 x와 y의 관계를 가장 잘 나타내는 직선을 그리는 것을 의미한다.
여기서 x는 독립적으로 변할 수 있는 독립 변수, y는 x 값에 의해 종속적으로 결정되므로 종속 변수에 해당한다.
독립 변수 x가 1개인 단순 선형 회귀와 Pytorch 구현에 대해서는 아래 게시글에 설명되어있다.
https://daeunnniii.tistory.com/192
[ML] 선형 회귀 (Linear Regression) 정리 & Pytorch 구현
선형 회귀(Linear Regression) 선형 회귀는 주어진 데이터로부터 x와 y의 관계를 가장 잘 나타내는 직선을 그리는 것을 의미한다. 여기서 x는 독립적으로 변할 수 있는 독립 변수, y는 x 값에 의해 종속
daeunnniii.tistory.com
다중 선형 회귀 분석(Multiple Linear Regression Analysis)
선형회귀에서 독립 변수 x가 2개 이상이면 다중 선형 회귀이다. 다수의 요소 x1, x2, ..., xn을 가지고 y 값을 예측한다. 예를 들어 오존 농도를 예측하는 모델을 만든다고 가정하면, 일조량, 기온, 풍속 등의 요소를 고려하여 오존 농도를 예측할 수 있다.
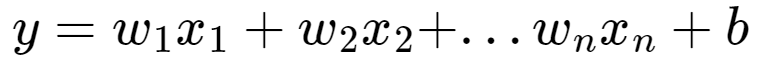
위 식은 아래와 같이 두 벡터의 내적으로 표현할 수 있다.
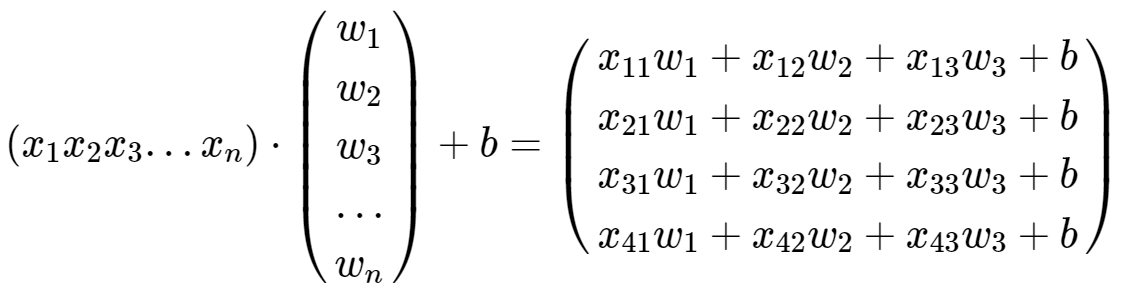
두 벡터를 각각 X와 W로 표현한다면 간단하게 $ H(X) = XW + b $ 로 표현할 수 있다.
1. 다중선형회귀 예시
다중선형회귀의 예시로 3개의 퀴즈 점수로부터 최종 점수를 예측하는 모델을 만들어볼 것이다. 샘플의 개수는 총 5개이고, 특성(feature)의 개수는 3개이다.
| Quiz 1 | Quiz 2 | Quiz 3 | Final |
| 73 | 80 | 75 | 152 |
| 93 | 88 | 93 | 185 |
| 89 | 91 | 80 | 180 |
| 96 | 98 | 100 | 196 |
| 73 | 66 | 70 | 142 |
다중선형회귀 구현
x_train의 크기가 5 X 3 이므로 가중치 W의 크기는 (3 x 1) 벡터이다.
또한 앞에서 단순선형회귀와 다르게 다중선형회귀에서는 가설(hypothesis)을 행렬곱으로 정의하였으므로 matmul()을 사용한다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# training 데이터 선언 - (5 X 3) 행렬 X와 (5 X 1) 행렬 Y 선언
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# 모델 초기화 - 가중치 W와 편향 b를 0으로 초기화한다.
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=1e-5)
epochs = 20
for e in range(epochs + 1):
# H(x) 계산
# 편향 b는 브로드 캐스팅되어 각 샘플에 더해진다.
hypothesis = x_train.matmul(W) + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
e, epochs, hypothesis.squeeze().detach(), cost.item()
))결과는 다음과 같다.
Epoch 0/20 hypothesis: tensor([0., 0., 0., 0., 0.]) Cost: 29661.800781
Epoch 1/20 hypothesis: tensor([67.2578, 80.8397, 79.6523, 86.7394, 61.6605]) Cost: 9298.520508
Epoch 2/20 hypothesis: tensor([104.9128, 126.0990, 124.2466, 135.3015, 96.1821]) Cost: 2915.712402
Epoch 3/20 hypothesis: tensor([125.9942, 151.4381, 149.2133, 162.4896, 115.5097]) Cost: 915.040527
Epoch 4/20 hypothesis: tensor([137.7967, 165.6247, 163.1911, 177.7112, 126.3307]) Cost: 287.936096
Epoch 5/20 hypothesis: tensor([144.4044, 173.5674, 171.0168, 186.2332, 132.3891]) Cost: 91.371063
Epoch 6/20 hypothesis: tensor([148.1035, 178.0143, 175.3980, 191.0042, 135.7812]) Cost: 29.758249
Epoch 7/20 hypothesis: tensor([150.1744, 180.5042, 177.8509, 193.6753, 137.6805]) Cost: 10.445267
Epoch 8/20 hypothesis: tensor([151.3336, 181.8983, 179.2240, 195.1707, 138.7440]) Cost: 4.391237
Epoch 9/20 hypothesis: tensor([151.9824, 182.6789, 179.9928, 196.0079, 139.3396]) Cost: 2.493121
Epoch 10/20 hypothesis: tensor([152.3454, 183.1161, 180.4231, 196.4765, 139.6732]) Cost: 1.897688
Epoch 11/20 hypothesis: tensor([152.5485, 183.3609, 180.6640, 196.7389, 139.8602]) Cost: 1.710552
Epoch 12/20 hypothesis: tensor([152.6620, 183.4982, 180.7988, 196.8857, 139.9651]) Cost: 1.651416
Epoch 13/20 hypothesis: tensor([152.7253, 183.5752, 180.8742, 196.9678, 140.0240]) Cost: 1.632369
Epoch 14/20 hypothesis: tensor([152.7606, 183.6184, 180.9164, 197.0138, 140.0571]) Cost: 1.625924
Epoch 15/20 hypothesis: tensor([152.7802, 183.6427, 180.9399, 197.0395, 140.0759]) Cost: 1.623420
Epoch 16/20 hypothesis: tensor([152.7909, 183.6565, 180.9530, 197.0538, 140.0865]) Cost: 1.622152
Epoch 17/20 hypothesis: tensor([152.7968, 183.6643, 180.9603, 197.0618, 140.0927]) Cost: 1.621262
Epoch 18/20 hypothesis: tensor([152.7999, 183.6688, 180.9644, 197.0661, 140.0963]) Cost: 1.620501
Epoch 19/20 hypothesis: tensor([152.8014, 183.6715, 180.9665, 197.0686, 140.0985]) Cost: 1.619757
Epoch 20/20 hypothesis: tensor([152.8020, 183.6731, 180.9677, 197.0699, 140.0999]) Cost: 1.619046
2. Pytorch의 nn.Module을 이용하여 다중 선형회귀 구현하기
위에서는 다중선형회귀를 이해하기 위해 가설, 비용함수를 직접 정의해서 Pytorch에서는 선형회귀 모델은 nn.Linear(), 평균 제곱 오차는 nn.functional.mse_loss()라는 함수로 구현되어있다. 이번에는 nn.Module을 이용해 선형회귀 모델을 클래스로 구현해볼 것이다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class MulLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1) # 다중 선형 회귀이므로 input_dim=3, output_dim=1.
def forward(self, x):
return self.linear(x)
# training 데이터 선언 - (5 X 3) 행렬 X와 (5 X 1) 행렬 Y 선언
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
model = MulLinearRegressionModel()
print(list(model.parameters()))
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5) # optimizer 설정
epochs = 10000
for e in range(epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad() # gradient를 0으로 초기화한다.
cost.backward() # 비용 함수를 미분하여 gradient를 계산한다.
optimizer.step() # W와 b를 업데이트
# 1000번마다 로그 출력
if e % 1000 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
e, epochs, cost.item()
))
print(list(model.parameters())) # 최적화된 가중치 W와 편향 b 값 확인결과는 다음과 같다. 10000번 epoch를 반복한 결과 cost의 값이 최종적으로 매우 작아졌다.
최적화된 가중치 W의 값은 [0.9342, 0.5209, 0.5548], 편향 b의 값은 0.1887이다.
[Parameter containing:
tensor([[-0.3042, 0.2968, -0.3065]], requires_grad=True), Parameter containing:
tensor([0.1698], requires_grad=True)]
Epoch 0/10000 Cost: 39676.117188
Epoch 1000/10000 Cost: 4.919497
Epoch 2000/10000 Cost: 2.944014
Epoch 3000/10000 Cost: 1.794331
Epoch 4000/10000 Cost: 1.125005
Epoch 5000/10000 Cost: 0.735076
Epoch 6000/10000 Cost: 0.507656
Epoch 7000/10000 Cost: 0.374799
Epoch 8000/10000 Cost: 0.296958
Epoch 9000/10000 Cost: 0.251132
Epoch 10000/10000 Cost: 0.223968
[Parameter containing:
tensor([[0.9342, 0.5209, 0.5548]], requires_grad=True), Parameter containing:
tensor([0.1887], requires_grad=True)]
3. 새로운 데이터 예측해보기
훈련 데이터 중 하나인 73, 80, 75를 입력으로 넣어 예측해보았다.
new_var = torch.FloatTensor([[73, 80, 75]]) # 새로운 데이터 생성
pred_y = model(new_var) # forward 연산
print("훈련 후 입력이 73, 80, 75일 때의 예측값 :", pred_y)실제 결과값 152와 가깝게 나온 것을 확인할 수 있다.
훈련 후 입력이 73, 80, 75일 때의 예측값 : tensor([[151.6657]], grad_fn=<AddmmBackward0>)
임의의 값 [89, 78, 90]을 선정하여 모델의 입력으로 넣었다.
new_var = torch.FloatTensor([[89, 78, 90]]) # 새로운 데이터 생성
pred_y = model(new_var) # forward 연산
print("훈련 후 입력이 89, 78, 90일 때의 예측값 :", pred_y)그 결과 위 [73, 80, 75]의 예측값인 151.66보다 큰 예측값 173.89를 반환한 것을 확인할 수 있다.
훈련 후 입력이 89, 78, 90일 때의 예측값 : tensor([[173.8924]], grad_fn=<AddmmBackward0>)
참고:
- 위키독스 Pytorch로 시작하는 딥러닝 입문
- 위키독스 딥 러닝을 이용한 자연어 처리 입문
'AI > 머신러닝' 카테고리의 다른 글
| [Pytorch] 소프트맥스 회귀(Softmax Regression) 구현 & MNIST 분류 적용 (0) | 2023.05.14 |
|---|---|
| [ML] 다중 클래스 분류(Multi-Class Classification) 정리 (0) | 2023.05.12 |
| [ML] 로지스틱 회귀(Logistic Regression) 쉽게 이해하기 & Pytorch 구현 (0) | 2023.04.09 |
| [ML] 선형 회귀 (Linear Regression) 정리 & Pytorch 구현 (0) | 2023.04.09 |
| Microsoft Azure Machine Learning Studio(classic) 사용법과 자동차 가격 예측 (1) | 2020.08.27 |